Turing Complete: From Logical Gates to CPU Architecture
In 2021, LevelHead published Turing Complete, a game about computer science. My friend Christophe Georgescu recommended me to play it. Unfortunately, I took his advice and now I can not stop to play this game! The game challenges you to design an entire computer from scratch. You start with basic logic gates, then move on to components, memory, CPU architecture, and finally assembly programming. By the way, the game is neat and present all these concepts in a playful and intuitive way.
Truth Tables
A truth table shows how the truth or falsity of a compound statement depends on the truth or falsity of the simple statements from which it is constructed.
Example with the AND gate:
| Input 1 | Input 2 | Output |
|---|---|---|
| ❌ | ❌ | ❌ |
| ✅ | ❌ | ❌ |
| ❌ | ✅ | ❌ |
| ✅ | ✅ | ✅ |
Input and Output will often be represented with variable names, like in algebra. And instead of using colors, you will often see the values represented as 0/1 or False/True.
Logical Gates
It turns out tht you can build all the logic for a computer out of either NAND or NOR gates. The Apollo guidance computers, were built entirely of NOR gates. Designed in the sixties, they had only 4KB of RAM and 32KB of disk space, but guided astronauts to the moon nonetheless.
Modern computers are not built entirely of just one of the logical gates, but when applicable NAND gates are prefered over NOR, because they have less delay and occupy less area.

NAND gate
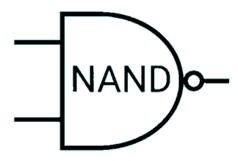
1 unless both inputs are 1.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
AND gate
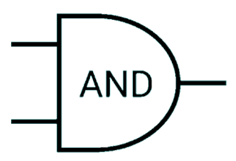
1 when both inputs are 1.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
OR gate
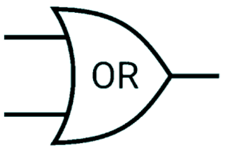
1 when either input is 1
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
NOR gate
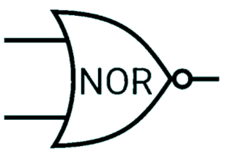
1 when neither inputs are 1.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR gate
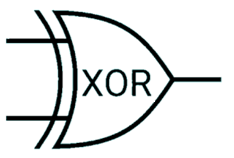
1 when inputs are different
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR gate

1 when inputs are the same.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Buffer
Outputs this tick's input, next tick.
NOT gate
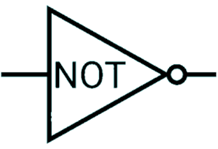
Inverts the input.
| Input | Output |
|---|---|
| 0 | 1 |
| 1 | 0 |
De Morgan's Laws
The truth tables of the four fundamental gates are symmetrical. You can convert betwee, them by inverting the input (vertical arrows) or inverting the output (horizontal arrows) as indicated by the graphic below.
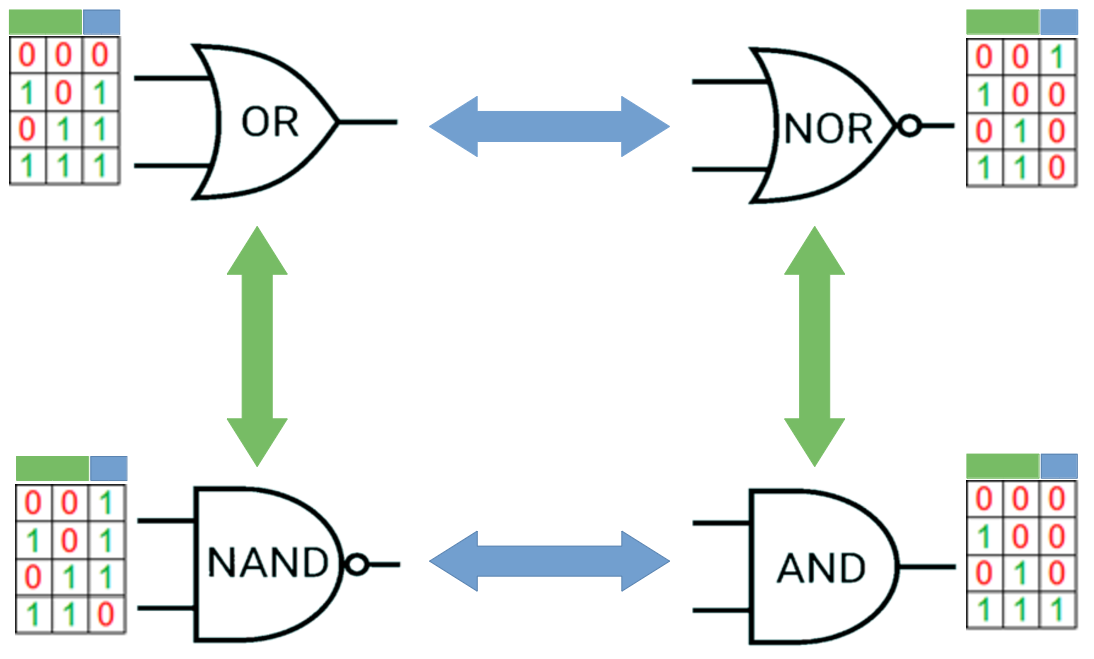
Notes:
- You can get from any basic gate to any other, at most you have to
NOTboth inputs and output. - You can go between
OR/NORby inverting output. The same goesAND/NAND. In factNORmeansNOTORandNANDmeansNOT AND. Notice the component shape ofOR/NORare identical except for the little dot at the tip which meansNOT.AND/NANDare also identical except for this dot. - Negating the output flips all the bits in the last row of the truth table. Negating the inputs mirrors the last row of the truth table around the center.
Arithmetic Logic Unit
Memory
CPU Architecture
Assembly
References
https://www.nand2tetris.org/
https://turingcomplete.game
Relevant Tags
About the Author
Latest Articles
-
Research Tax Credit
The Research Activities Tax Credit is a tax credit that incentivizes private companies to increase their Research and Development (R&D). Within my company, I have been tasked with writing the Research Tax Credit (CIR) justification report for France. Here, the method for writing such a report.OCT 2025 · PIERRE-EDOUARD GUERIN -
Turing Complete: From Logical Gates to CPU Architecture
In 2021, LevelHead published Turing Complete, a game about computer science. My friend Christophe Georgescu recommended me to play it. Unfortunately, I took his advice and now I can not stop to play this game! The game challenges you to design an entire computer from scratch. You start with basic logic gates, then move on to components, memory, CPU architecture, and finally assembly programming. By the way, the game is neat and present all these concepts in a playful and intuitive way.SEP 2025 · PIERRE-EDOUARD GUERIN -
How to Manage a Project?
In any company, every task is part of a project. I am responsible for managing multiple projects each year. I have to present deliverables to stakeholders, meet deadlines, allocate mandays and coordinate everyone’s actions. This is a meticulous work that requires a strong methodology.JUN 2025 · PIERRE-EDOUARD GUERIN